Image-to-Image Projections

2D Transformation

Projective Transformation Matrix

For 2D images it's a 3x3 matrix applied to homogeneous coordinates $$\begin{bmatrix} x' \\ y' \\ w' \end{bmatrix} = \begin{bmatrix} a & b & c \\ d & e & f \\ g & h & i \end{bmatrix} \begin{bmatrix} x \\ y \\ w \end{bmatrix}$$

Special Projective Transformations

These are homogeneous coordinates

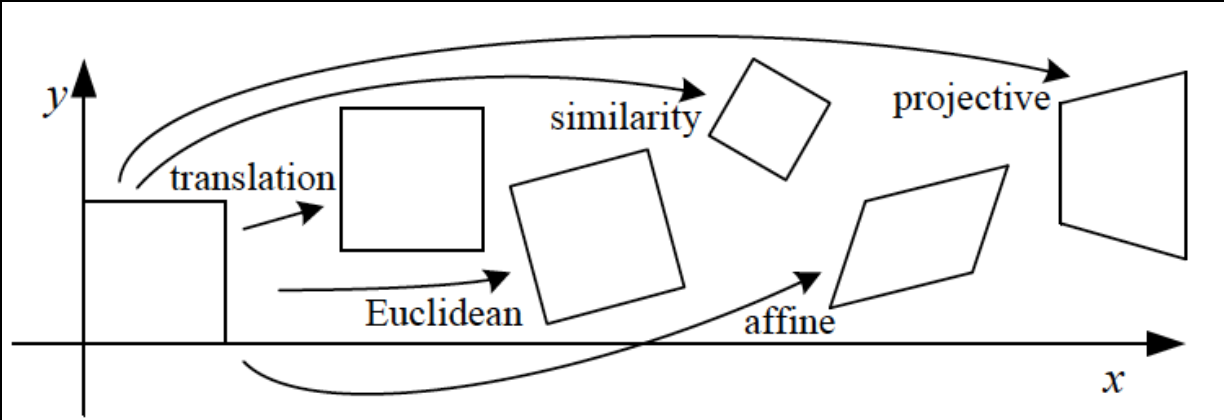
Translation

$$\begin{bmatrix} x' \\ y' \\ 1 \end{bmatrix} = \begin{bmatrix} 1 & 0 & t_x \\ 0 & 1 & t_y \\ 0 & 0 & 1 \end{bmatrix} \begin{bmatrix} x \\ y \\ 1 \end{bmatrix}$$

Preserves:

• Length/Areas
• Angles
• Orientation
• Lines

Number of pairs of points needed to compute: 1 (2 unknowns)

Euclidean

$$\begin{bmatrix} x' \\ y' \\ 1 \end{bmatrix} = \begin{bmatrix} \cos(\theta) & -\sin(\theta) & t_x \\ \sin(\theta) & \cos(\theta) & t_y \\ 0 & 0 & 1 \end{bmatrix} \begin{bmatrix} x \\ y \\ 1 \end{bmatrix}$$

Preserves:

• Length/Areas
• Angles
• Lines

Number of pairs of points needed to compute: 2 (3 unknowns)

Similarity

$$\begin{bmatrix} x' \\ y' \\ 1 \end{bmatrix} = \begin{bmatrix} a\cos(\theta) & -a\sin(\theta) & t_x \\ a\sin(\theta) & a\cos(\theta) & t_y \\ 0 & 0 & 1 \end{bmatrix} \begin{bmatrix} x \\ y \\ 1 \end{bmatrix}$$

Preserves:

• Ratios of Areas
• Angles
• Lines

Number of pairs of points needed to compute: 2 (4 unknowns)

Affine

$$\begin{bmatrix} x' \\ y' \\ 1 \end{bmatrix} = \begin{bmatrix} a & b & c \\ d & e & f \\ 0 & 0 & 1 \end{bmatrix} \begin{bmatrix} x \\ y \\ 1 \end{bmatrix}$$

Preserves:

• Parallel lines
• Ratio of Areas
• Lines

Number of pairs of points needed to compute: 3 (6 unknowns)

Homography

$$\begin{bmatrix} x' \\ y' \\ 1 \end{bmatrix} = \begin{bmatrix} wx' \\ wy' \\ w \end{bmatrix} = \begin{bmatrix} a & b & c \\ d & e & f \\ g & h & 1 \end{bmatrix} \begin{bmatrix} x \\ y \\ 1 \end{bmatrix}$$

Preserves:

• Lines

Number of pairs of points needed to compute: 4 (8 unknowns)